Representasi Angka, Signed-Unsigned, dan Casting di C
Memahami detail tentang bagaimana operasi antar bilangan dengan modifier Signed ataupun Unsigned penting untuk pemrogram agar dapat menghindari hal yang tidak terduga, bug ataupun celah keamanan.
Karena tidak semua bahasa pemrograman menyediakan modifier Signed dan Unsigned yang digunakan untuk menentukan bagaimana bit dalam tipe data tersebut dibaca, maka disini saya akan menggunakan bahasa pemrograman C, karena menyediakan dua modifier tersebut sehingga cocok digunakan sebagai contoh.
Contoh kasus dalam melakukan operasi perbandingan menggunakan bahasa C ketika membandingkan dua angka yang memiliki modifier berbeda seperti -1 < 2u (tanda u diartikan unsigned, dan tanpa tanda diartikan signed) maka hasilnya akan 0 atau false, padahal secara matematis -1 kurang dari 2 adalah benar atau true atau 1.
Di dalam tulisan ini saya akan membahas beberapa poin sehingga kita bisa melihat lebih dekat terkait kasus tersebut, antara lain
- Bagaimana angka disimpan di dalam memory
- Perbedaan signed dan unsigned
- Zero Expanding dan Signed Expanding
- Truncating Number
Binary Digit
Komputer menyimpan atau membaca semua data seperti angka, huruf, gambar atau video dalam unit terkecil yaitu Bytes, dalam 1 Bytes terdiri dari 8 bit.
Bit merupakan sistem bilangan dengan basis 2, artinya hanya ada dua simbol yang digunakan yaitu 0 dan 1. Sebagai perbandingan, kita selama ini mengenal Desimal yaitu sistem bilangan dengan basis 10, artinya ada 10 simbol yang digunakan yaitu 0 hingga 9, selain itu ada juga hexadesimal yaitu sistem bilangan dengan basis 16, dengan simbol 0-9 dan a-f.
Hexadesimal biasanya digunakan untuk merepresentasikan alamat memory karena lebih ringkas. Satu hex digit terdiri dari 4 bit, jadi dua hex digit sama dengan 1 bytes atau 8 bit, karena, angka maksimal dari 4 bit bisa dituliskan dengan 1111, dalam desimal akan sama dengan $2^3+2^2+2^1+2^0 = 15$, hex digit paling besar adalah F yang dalam desimal akan sama dengan 15.
Bagaimana urutan Bytes data dituliskan dalam memory tergantung dari arsitekturnya. Terdapat dua cara komputer dalam menuliskan urutan Bytes di dalam memory, yaitu Big-Endians dan Little-endians. Big-Endians artinya MSB (Most Significant Bytes) atau Bytes yang memiliki nilai paling besar berada di sebelah paling kanan (alamat memory paling rendah), sedangkan Little-Endians artinya LSB (Least Significant Bytes) atau Bytes yang memiliki nilai paling kecil berada di sebelah paling kanan (alamat memory paling rendah).
Contohnya, untuk nilai hex 0x12345678
Dalam Big-Endians, dalam memory akan disimpan dalam urutan 12 34 56 78, sedangkan dalam Little-Endians, dalam memory akan disimpan dalam urutan 78 56 34 12.
Signed dan Unsigned
Di bahasa C terdapat dua modifier yang digunakan untuk menentukan bagaimana bit dalam tipe data tersebut diartikan yaitu Signed dan Unsigned.
Unsigned hanya menyimpan bilangan postif, sedangkan Signed bisa menyimpan bilangan positif dan negatif.
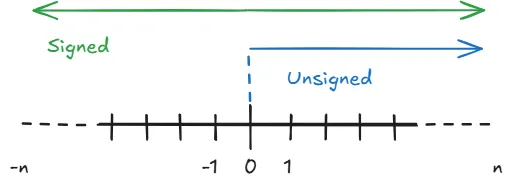
Positif dan negatif di modifier Signed akan ditentukan oleh bit dengan nilai paling besar (MSB), jika 0 maka positif dan jika 1 maka negatif.
Sedangkan dalam penulisan bit untuk modifier Unsigned, semua bit akan dianggap sebagai positif. Contohnya dalam table berikut
| Hex | Binary | B2U(x) [unsigned] | B2T(x) [signed] |
|---|---|---|---|
| 0xA | 1010 | 2³ + 2¹ = 10 | -2³ + 2¹ = -6 |
| 0x1 | 0001 | 2⁰ = 1 | 2⁰ = 1 |
| 0xB | 1011 | 2³ + 2¹ + 2⁰ = 11 | -2³ + 2¹ + 2⁰ = -5 |
| 0x2 | 0010 | 2¹ = 2 | 2¹ = 2 |
| 0x7 | 0111 | 2² + 2¹ + 2⁰ = 7 | 2² + 2¹ + 2⁰ = 7 |
| 0xC | 1100 | 2³ + 2² = 12 | -2³ + 2² = -4 |
Dalam table diatas kita bisa lihat bahwa dengan bit yang sama, konversi ke desimal bisa berbeda tergantung angka tersebut memiliki modifier Signed atau Unsigned.
Karena Signed dan Unsigned memiliki representasi bit yang berbeda maka kita perlu hati hati ketika melakukan perbandingan antara bilangan Signed dan Unsigned, karena ketika membandingkan angka dengan modifier yang berbeda, dalam kasus ini bilangan Signed akan dikonversi ke Unsigned secara implisit sebelum melakukan perbandingan.
Maka dari itu kenapa -1 < 2u hasilnya false, karena -1 akan dikonversi ke unsigned secara implisit sehingga memiliki nominal yang berbeda dari yang seharusnya. -1 dalam binary 4 bit akan direpresentasikan sebagai 1111 ( $-2^3 + 2^2 + 2^1 + 2^0 = -1$ ) lalu ketika dikonversi ke unsigned akan bernilai 15 ($U_{max}$) ( $2^3 + 2^2 + 2^1 + 2^0 = 15$ ) dan ketika dibandingkan menjadi 15 < 2, hasilnya false.
Dalam menghitung angka maksimum dari Unsigned number bisa menggunakan rumus $U_{max} = 2^{w}-1$ dan $U_{min} = 0$
Dalam menghitung angka maksimum dan minimum dari Signed number bisa menggunakan rumus $T_{min} = -2^{w-1}$ dan $T_{max} =2^{w-1}-1$
$w$ adalah jumlah bit yang digunakan dalam tipe data yang digunakan, misalnya di bahasa C dalam sistem 64 bit
| Type (signed) | Type (unsigned) | Bytes | Bit (1 Bytes = 8 Bit) |
|---|---|---|---|
| char | unsigned char | 1 | 8 |
| short | unsigned short | 2 | 16 |
| int | unsigned | 4 | 32 |
| long | unsigned long | 8 | 64 |
| int32_t | uint32_t | 4 | 32 |
| int64_t | uint64_t | 8 | 64 |
| char * | 8 | 64 | |
| float | 4 | 32 | |
| double | 8 | 64 |
Dari table diatas ketika kita menggunakan unsigned char untuk menampung nilai, maka angka maksimum yang bisa disimpan dalam tipe tersebut yaitu $U_{max} = 2^w - 1 = 2^8 - 1 = 255$
Promotions
Di bahasa C, sebelum ekspresi aritmatika atau perbandingan dievaluasi, compiler akan melakukan proses yang disebut dengan Usual Arithmetic Conversions. Aturan tersebut menentukan bagaimana dua operand dengan tipe data berbeda ‘disamakan` sebelum dihitung.
Aturan pertama, jika semua tipe data lebih kecil dari int seperti char, short, maka akan dipromosikan atau dikonversi ke int atau unsigned int.
Aturan kedua, jika tipe data sama, maka akan langsung dilakukan perbandingan.
Aturan ketiga, jika memiliki modifier yang berbeda (signed dan unsigned) maka
- Jika
unsignedoperand punya ukuran yang lebih besar atau sama dengansignedoperand, makasignedoperand akan dikonversi keunsigned - Jika
signedoperand bisa menampung atau punya ukuran lebih besar dariunsignedoperand (misalnyasigned long longkeunsigned int) makaunsignedoperand akan dikonversi kesigned - Selain itu, maka
signedoperand akan dikonversi keunsigned
Contoh kasus
-1 < 2u- -1 adalah
signed int - 2 adalah
unsigned int - Karena salah satu ada modifier
unsignedmaka semua akan ‘disamakan’ menjadiunsignedatau operandsignedakan dikonversi menjadiunsigned
- -1 adalah
-1LL < 2u- -1 adalah
signed long long - 2 adalah
unsigned int - Karena ukuran
long longlebih besar dariintmaka operandunsigned intakan dikonversi menjadisigned long long
- -1 adalah
-1LL < 2ULL- -1 adalah
signed long long - 2 adalah
unsigned long long - Karena ukuran keduanya sama yaitu
long longmaka operandsigneddikonversi menjadiunsigned
- -1 adalah
Zero Expanding dan Signed Expanding
Ada kasus dimana kita perlu menambah ukuran tipe data menjadi lebih besar, dengan memindahkan atau casting dari tipe data dengan ukuran lebih kecil ke tipe data dengan ukuran lebih besar, misalnya kita perlu angka yang lebih besar dari tipe data int (32 bit) maka kita akan konversi ke tipe data long (64 bit).
Di modifier Unsigned, secara otomatis akan ditambahkan 0 di bit paling kiri (MSB) sehingga tidak akan mengubah nilai aslinya. Di modifier Signed, akan ditambahkan sesuai dengan sign-nya, misalnya negatif maka akan ditambahkan 1 sebanyak selisihnya sehigga secara nilai juga tidak berubah. Contoh
| 8 bit | 16 bit | |
|---|---|---|
| 12 (unsiged) | 0000 1100 | 0000 0000 0000 1100 |
| -12 (signed) | 1111 0100 | 1111 1111 1111 0100 |
Truncating Number
Kebalikan dari zero expanding dan sign expanding, ada beberapa kasus pemindahan data dari tipe data dengan size besar ke tipe data dengan size lebih kecil.
Konsepnya sama dengan expanding, hanya saja bit yang paling kiri (MSB) akan dihilangkan sesuai dengan total bit penampung barunya. Contoh, dari 8 bit (0000 0001) ke 4 bit jadinya 0001, bit paling depan (MSB) dipotong.
Disini saya akan membuat contoh untuk memindahkan data dari 16 bit ke 8 bit, untuk data signed 8 bit, maksimal data yang bisa ditampung yaitu 127 dan minimal data yang bisa ditampung yaitu -128.
Kasus pertama, jika kita memindahkan data dari 16 bit ke 8 bit, tapi datanya masih bisa ditampung di 8 bit
int main(){
int16_t x16 = 101;
int8_t x8 = x16;
printf("16 bit: %d, 8 bit: %d\n", x16, x8); // 16 bit: 101, 8 bit: 101
return 0;
}Angka 101, jika kita tampung dalam 16 bit akan terlihat seperti gambar dibawah ini
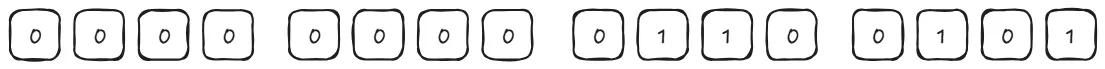
Lalu, kita pindahkan ke tipe data 8 bit, maka 8 bit paling kiri (MSB) akan dihapus

Karena 101 kurang dari angka maksimal yang ditampung 8 bit, maka tidak ada perubahan nilai.
Kasus kedua, jika kita memindahkan data dari 16 bit ke 8 bit yang melebihi angka yang bisa ditampung 8 bit.
int main(){
int16_t x16 = 1000;
int8_t x8 = x16;
printf("16 bit: %d, 8 bit: %d\n", x16, x8); // 16 bit: 1000, 8 bit: -24
return 0;
}Angka 1000, jika kita tampung dalam 16 bit akan terlihat seperti gambar dibawah ini
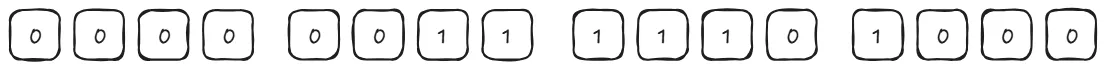
Lalu, kita pindahkan ke tipe data 8 bit

Berbeda dengan kasus pertama, dalam kasus ini, tipe data dengan 8 bit tidak dapat menampung angka 1000 sehingga terjadi perubahan nilai. Jika kita coba hitung manual maka hasilnya adalah
$-1x2^7+1x2^6+1x2^5+1x2^3 = -128 + 64 + 32 + 8 =-24$
Cara lain, kita bisa mencari angka perpindahan dengan rumus $value\ mod\ 2^w$, $value$ adalah angka yang akan ditampung, $mod$ adalah modulus dan $2^w$ adalah max kombinasi untuk penampung barunya. Contoh dalam kasus pertama jika kita hitung untuk value 101 dan $2^w$ untuk tipe data 8 bit adalah 256 kombinasi
$101\ mod\ 256$ hasilnya tetap 101, karena 101 kurang dari 256 jadi tipe data 8 bit masih bisa menampung.
Contoh lain dalam kasus kedua, value 1000 dan $2^w$ untuk tipe data 8 bit adalah 256 kombinasi
$1000\ mod\ 256$ hasilnya 232, karena 232 < (256-1) maka hasilnya 232, tapi berbeda ketika ditampung dengan modifier Signed, artinya angka positif maksimal yang bisa ditampung adalah 127, dan karena hasil ≥ $2^{w-1}$ atau 232 ≥ 127 maka harus dikurangkan dengan $2^w$ bisa ditulis dengan rumus $signedValue = usignedValue - 2^w$
232 - 256 = -24
Bryant, R. E., & O’Hallaron, D. R. (2021). Computer systems: A programmer’s perspective (4th ed.). Pearson.
- Signed
- Unsigned
- Casting
- C Programming Language